AD-TECH
- リクルートデータ組織のブログをはじめました。※最新情報はRecruit Data Blogをご覧ください。
- Recruit Data Blogはこちら
汎用人型雑用AIの stakaya です。
たまたま数年前に社内のBLOGに書いたABテストのロジックのまとめ&比較記事を発掘したので、 このまま眠らせているのはもったいないぞと、 圧倒的もったいない精神を発揮し、シェアさせていただきます。
あの頃は私も若かった。
社内では”堅物・真面目・一途”で有名なものでして、下記文章がお硬いのはご勘弁ください。
はじめに
本記事は、施策の評価手法としてしばしば用いられるA/Bテスト(A/B testing)について、できる限り背後にある仮定を明記した上で、まとめたものである。
A/Bテストとは、主にインターネットマーケティングにおける施策の良否を判断するために、2つの施策(通常、A・Bと記載)を比較する行為を指すものである。
具体的には
- ウェブサイト内の一部分を変更し、変更前(A)と変更後(B)のどちらがよりコンバージョンに結びつくかを計測
- 広告クリエイティブを均等に出し、広告Aと広告Bのどちらがよりコンバージョンに結びつくかを計測
等の状況を想像すれば良い。
通常、書籍やインターネット上のコンテキストにおいて言及されるA/Bテストの評価基準は、”クリック数(率)“が主に使われ、この評価基準に対して統計的検定、特にχ2検定がしばしば使用されるものの、 標本(サンプル、A/Bテストの結果得られるデータ)に対する確率分布などの性質に関する仮定を明記しないものがほとんどである。
更に、実務においては、CTR・CVRなどの指標のどれを重視するのかという議論は残るが、 最終的なコンバージョンを重視し”セッションあたりの平均売上・利益額”等の連続的な数値が評価基準となるケースも存在する。
本記事においては、このような複数の状況に対し「何が妥当な統計検定手法となるのか?」についてをまとめる。
A/Bテストにおいて使用される統計検定手法について
まず、A/Bテストにおいて使用される検定手法について、以下の表1にまとめた。
表1においては、各統計検定手法について
- どのような条件下ならば使ってよいか
- 他の統計検定手法との関連性
についてもまとめている。
表1:A/Bテストに使われる検定手法
| 手法名 | 対象となるデータ | 使用可能条件 | その他 |
|---|---|---|---|
| 二項検定 | クリック数(コンバージョン率) | 常に使える | 理論的に厳密。フィッシャーの正確確率検定に対して、”戻しの処理”を加えたもの。復元抽出。 |
| (ピアソンの)χ2検定 | クリック数(コンバージョン率) | サンプルサイズが大きい場合(>O(10)) | 二項検定において、分布(二項分布)をサンプルサイズが大きい極限において正規分布で近似(中心極限定理) |
| フィッシャーの正確確率検定 | クリック数(コンバージョン率) | 常に使える | 理論的に厳密。二項検定とは違い、抽出したサンプルを戻さないと考える。非復元抽出。 |
| (対応のない)t検定 | クリック数(コンバージョン率) 売上等の連続的な数値 |
クリック数の場合:サンプルサイズが大きい 連続数値の場合:分布が正規分布 or サンプルサイズが大きい |
クリック数の場合:サンプルサイズが大きい極限において正規分布で近似(中心極限定理) 連続数値の場合:平均値に差があるか否かの検定 |
| ウィルコクソンの順位和検定 | 売上等の連続的な数値 | サンプルサイズが大きい | 中央値に差があるか否かの検定 |
フィッシャーの正確確率検定と二項検定の違いは、”確率の考え方”による。 例えば、
- 黒飴ちゃんが10個
- 白飴ちゃんが10個
の合計20個の飴ちゃんが入っている箱を考え、そこから5個の飴ちゃんを抽出した際に、黒飴ちゃんが1個・白飴ちゃんが5個出現する確率を考える。 この時、各々検定の場合どのように確率を考えるのかをいうと
- フィッシャーの正確確率検定の場合
- 箱から飴ちゃんが減っていく分を加味して確率を計算
- 確率=10/20 * 10⁄19 * 9⁄18 * 8⁄17 * 7⁄16 * 6⁄15 * 5⁄15 * (並べ方の総数(5))
- 二項検定の場合
- 箱から飴ちゃんが減っていく効果を加味しない
- 飴ちゃんを抽出後、”戻す”。従って、常に白 or 黒飴ちゃんが出る確率は10/20
- 確率=10/20 * 10⁄20 * 10⁄20 * 10⁄20 * 10⁄20 * 10⁄20 * (並べ方の総数(5))
ということである。 この例だけ見ると「フィッシャーの正確確率検定の方が正確なのでは?」と思われるかもしれないが、コンバージョンの計算などにおいては、 コンバージョンするユーザが1人減ったからと言って、他の人のコンバージョンレートが下がるとは考え難く、”コンバージョンする確率は常に一定”と仮定する方が自然なので、二項検定を用いるほうが正しいと考えられる。
t検定とウィルコクソンの順位和検定との違いは検定統計量が平均値であるか(t検定)、または中央値(ウィルコクソンの順位和検定)であるかである。 ウィルコクソンの順位和検定においては、中央値で評価を行うため、少数の外れ値のために偽の有意な結果が出ることは、t検定に比べるとはるかに少なくなる。 従って、データの分布において、明らかなはずれ値が存在する場合にはウィルコクソンの順位和検定を用いるのが妥当であろう。
ここで表1に記載したように、クリック数(率)の評価に関する検定手法の関係・考え方としては
- (ちゃんとやるなら)二項検定 →(サンプルサイズが大きく、確率分布が正規分布で近似出来る)→χ2 or t検定
となっており、WEB界隈におけるA/Bテストにおいて、実質的にχ2検定がしばしば使われている理由だと推察される。
また、(ピアソンの)χ2検定は、「観察された事象の相対的頻度が、ある頻度分布に従う」 という帰無仮説を検定するものである(A/Bテストの場合、オリジナルパターンの分布と同じであるという仮説)一方、 t検定の方は(CVRなどの)平均値にA・Bパターン間で差があるかを調べるものである点が異なる。 分布を見るか、平均値を見るか、という点が異なるのである。
A/Bテストの実施法
以下では、出来るだけ仮定を明記する形でA/Bテストの実施法を、具体例も示した上で、紹介する。
評価基準として、クリック数を採用した場合
A/Bテストを、クリック数に対して適用する場合、主に使用される検定手法は以下の通りである。
- χ2検定
- 二項検定
- t検定
表1より、A/Bテストにかけられるデータのサンプルサイズが大きいことを暗に仮定していることになるが、Web関連のデータについては、ほぼほぼ問題ないと考えられる。 従って、これらの検定手法はほぼ同じ結果(有意か否か)を返すことが期待される。
R言語による統計検定の例1:施策が有意となる場合
ある施策Aを行ったところ、以下のような結果を得た。表中の数値はコンバージョンしたか・しなかったかの件数を表す。 また、施策Bが現在のサイトの数値であり、YESがコンバ―ジョンした件数、NOがコンバージョンしなかった件数を表す。
| 施策名 / コンバージョンしたか? | YES | NO |
|---|---|---|
| 施策A(改善案サイト) | 454 | 20,933 |
| 施策B(現状サイト) | 189 | 10,845 |
同施策実行結果をR言語で以下のように表現しておく。
> x <- cbind(c(454, 189), c(20933, 10845))
> rownames(x) <- c("A", "B")
> colnames(x) <- c("YES", "NO")
> x
YES NO
A 454 20933
B 189 10845
この時、施策Aが有意であるかをR言語を用いて検定する。 直感的に、このケースにおいてはCVR(ConVersion Rate)が
- 施策AのCVR 454/(454+20933)≒2.12%
- 施策BのCVR 189/(189+10845)≒1.71%
となるので、施策Aに効果はあっただろうことが直感的にもわかる。
χ2検定の場合
> chisq.test(x, correct=FALSE)
Pearson's Chi-squared test
data: x
X-squared = 6.291, df = 1, p-value = 0.01214
二項検定の場合
> p_a <- sum(x["A",])/sum(x)
> conversion_total <- sum(x[,"YES"])
> conversion_a <- x["A", "YES"]
> binom.test(conversion_a, conversion_total, p_a, "two.sided")
Exact binomial test
data: conversion_a and conversion_total
number of successes = 454, number of trials = 643, p-value = 0.01253
alternative hypothesis: true probability of success is not equal to 0.659665
95 percent confidence interval:
0.6691859 0.7410402
sample estimates:
probability of success
0.7060653
t検定の場合
> t.test(c(rep(1, x[1,1]), rep(0, x[1,2])), c(rep(1, x[2,1]), rep(0, x[2,2])))
Welch Two Sample t-test
data: c(rep(1, x[1, 1]), rep(0, x[1, 2])) and c(rep(1, x[2, 1]), rep(0, x[2, 2]))
t = 2.5937, df = 24442.86, p-value = 0.009499
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.001001424 0.007196525
sample estimates:
mean of x mean of y
0.02122785 0.01712887
注目すべきはp-valueであり、各検定手法のp-valueは、上記のコードの実行結果より
- χ2検定: 1.214%
- 二項検定: 1.253%
- t検定: 0.9499%
となっている。 これは、各々の検定のP値が1%程度となっていることから、どの検定手法においても「5%水準で有意」、 すなわち「施策Aには効果があった(※より正確には施策Aは施策Bとは有意に異なる)」と解釈される。 この後、「効果があることがわかったので、では、実際に効果がどのくらいあったか?」を計測すればよい。
さらに、各統計検定手法とも、p-valueの値がほぼ近しい値を取っており、 表1に記載した仮定や条件を満たせば、どの統計検定手法を使っても良いということが推察される。
R言語による統計検定の例2:施策が有意とならない場合
まったく同じことを、データだけ、
| 施策名 / コンバージョンしたか? | YES | NO |
|---|---|---|
| 施策A | 400 | 20,933 |
| 施策B | 189 | 10,845 |
と変更して実行した。このケースにおいてはCVR(ConVersion Rate)が
- 施策AのCVR 400/(400+20933)≒1.88%
- 施策BのCVR 189/(189+10845)≒1.71%
となるので、施策Aに効果があったかは、例1に比べて定かではない。 同様にR言語を用いてp-valueを計算させると
- χ2検定: 30.09%
- 二項検定: 31.76%
- t検定: 29.41%
となり、全ての統計検定手法において、p-value > 5%となっているため、 「5%水準で有意」とは言えず、従って「施策Bには効果があったとは言えない(※より正確にはCVRが有意に異なるとは言えない)」と解釈される。
評価基準として、連続的な数値(売上額など)を採用した場合
A/Bテストを、連続的な数値(売上額など)に対して、適用する場合、主に使用される検定手法は以下の通りである。
- t検定
- ウィルコクソンの順位和検定
従って、これらの検定手法は、手法の違いはあれど、ほぼ同じ結果(有意か否か)を返すことが期待される。
R言語による統計検定の例3:施策が有意となる場合
ある施策Aを行ったところ、1人 or 1セッションあたりのCharge(売上)の分布は以下のようになった(データは下記に示すように適当に生成)。 この施策Aには有意な効果があるだろうか? Bが現状のサイトを表す。
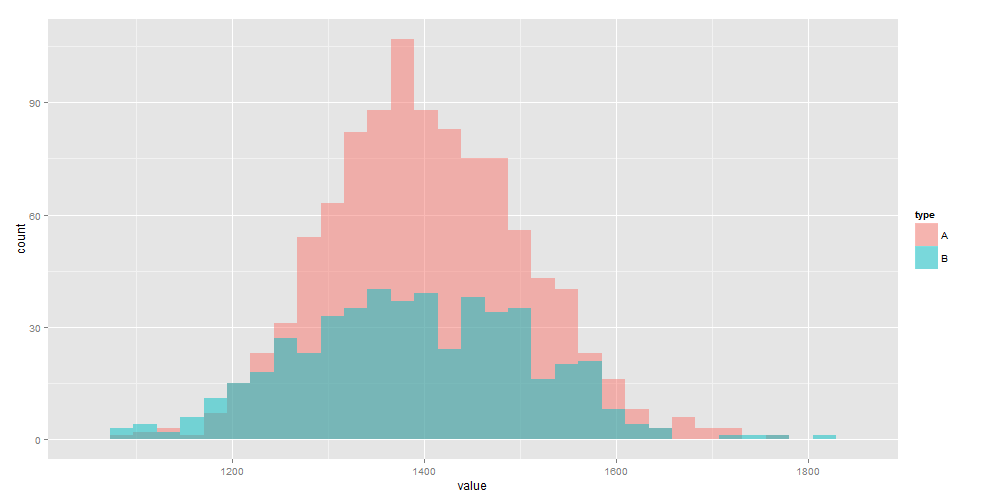
この時、施策Aが有意であるかをR言語を用いて検定する。 データは、
- 施策A:平均1,400, 標準偏差100の正規分布に従う1000個のデータ
- 施策B:平均1,385, 標準偏差120の正規分布に従う500個のデータ
として生成している。従って、実際に差がある確率分布からのデータである。
t検定の場合
> t.test(a, b)
Welch Two Sample t-test
data: a and b
t = 2.2055, df = 864.326, p-value = 0.02768
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1.534591 26.345401
sample estimates:
mean of x mean of y
1402.519 1388.579
ウィルコクソンの順位和検定の場合
> library(exactRankTests)
> wilcox.exact(a, b, paired=FALSE)
Asymptotic Wilcoxon rank sum test
data: a and b
W = 265532, p-value = 0.04953
alternative hypothesis: true mu is not equal to 0
各検定手法のp-valueは、上記のコードの実行結果より
- t検定: 2.768%
- ウィルコクソンの順位和検定:4.953%
となっている。従って、どちらの検定手法においても「5%水準で有意」、従って「施策Aには効果があった」と解釈される。
R言語による統計検定の例4:はずれ値を含む場合
取得したデータにはずれ値がある場合、特に、t検定など、 検定統計量として平均値を用いる場合、 結果がはずれ値の有無に強く依存してしまうため、はずれ値の処理を行う必要がある。 実務的には
- ある閾値をもとに、データの足切りを行う
といった対応が取られることが多い。 例3同様、施策Aに有意な効果があったか否かを検定する。データは
- 施策A:平均1,400, 標準偏差100の正規分布に従う1000個のデータ
- 施策B:平均1,400, 標準偏差100の正規分布に従う500個のデータ + 平均2,000, 標準偏差30の正規分布に従う25個のデータ(はずれ値)
として生成、下図のように分布している。
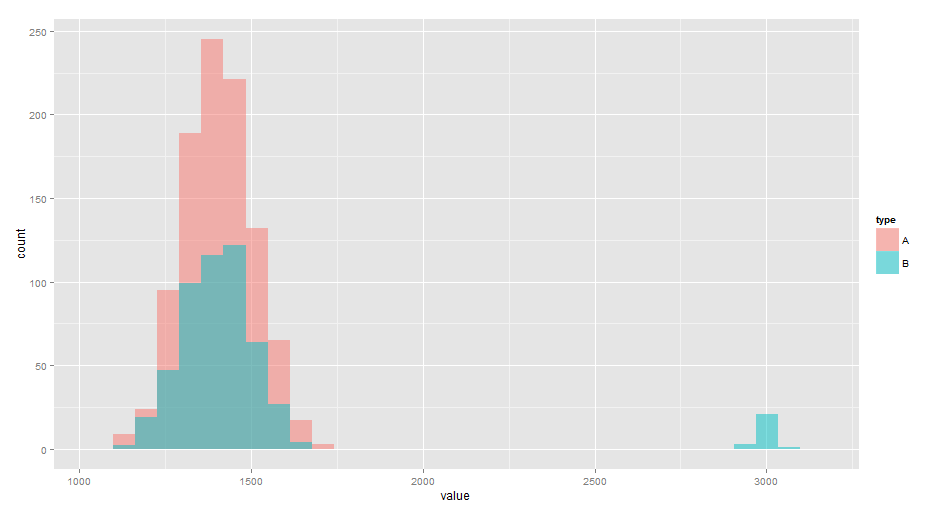
このデータを何も考えずにそのまま統計検定すると、各検定手法のp-valueは、上記のコードの実行結果より
- t検定: 1.319%
- ウィルコクソンの順位和検定:91.29%
となり、t検定においては「5%水準で有意」となっている一方、ウィルコクソンの順位和検定は有意という結果を示さない。 元のデータは、はずれ値を除くと同じ確率分布から生成したものであるので、 ウィルコクソンの順位和検定が正しい結果を返しており、t検定ははずれ値により、誤って”5%水準で有意”という結果を返してしまっている。
このようにはずれ値を含むデータに対して、平均値というはずれ値に弱い検定統計量を用いるt検定などの検定手法を使用する場合には、はずれ値を処理する必要がある。 はずれ値処理の一例として、平均値から3標準偏差以上かい離したデータは、ログ収集の際のミスだと判断し除去、 その後、同様にt検定・ウィルコクソンの順位和検定を適用すると、p-valueは
- t検定: 93.5%
- ウィルコクソンの順位和検定:99.8%
となり、両方の手法とも”有意”という結果を示さない。
まとめ
本記事ではA/Bテストについて、複数の統計検定手法の間の違い、およびその使用例を紹介した。 インターネット上でA/Bテストを行う場合には、「サンプルサイズが多い」という前提条件がほぼ成立するため、 巷で、
- クリック数に対して:χ2検定 or t検定
- 売上などの連続的な数値に対して:はずれ値に対処した上でt検定、またはノンパラメトリック検定(ウィルコクソンの順位和検定)
が使われているのは妥当であると考えられる。
また、統計検定手法の結果が、おおよそ一致していることも示した。 従って、どの手法を用いようが、施策が実際に有用なものならば、まさに”有意差は作られる”のである。 「Xという検定手法では有意にならなかったが、Yという検定手法手法では有意だった!」 などという本末転倒な議論を実務において行うことはナンセンスなのである。
参考
- A/Bテストについて
- 統計検定手法
- オンライン上のA/Bテストツール
広告
RCO アドテク部では、上の記事にダメ出しをしてくれる優秀な案件推進・人工知能開発エンジニア/データサイエンティストを募集しています。
TAGS :
#データ分析ARCHIVE
- 月別記事リストを見る
-
- 2020年03月 (2)
- 2019年09月 (3)
- 2019年08月 (1)
- 2019年06月 (1)
- 2019年03月 (5)
- 2019年02月 (3)
- 2018年09月 (1)
- 2018年06月 (2)
- 2018年05月 (2)
- 2018年04月 (1)
- 2018年02月 (1)
- 2018年01月 (1)
- 2017年12月 (2)
- 2017年11月 (1)
- 2017年10月 (1)
- 2017年08月 (1)
- 2017年07月 (2)
- 2017年06月 (1)
- 2017年05月 (3)
- 2017年04月 (5)
- 2017年03月 (12)
- 2017年02月 (16)
- 2017年01月 (1)
- 2016年12月 (1)
- 2016年08月 (1)
- 2016年06月 (5)
- 2016年05月 (2)
- 2016年04月 (1)
- 2016年03月 (3)
- 2016年02月 (8)
- 2016年01月 (3)
- 2015年12月 (2)
- 2015年03月 (1)
- 2015年02月 (2)
- 2015年01月 (3)
- 2014年12月 (2)
- 2014年11月 (3)
- 2014年10月 (1)
- 2014年09月 (2)
- 2014年07月 (1)
- 2014年04月 (2)
- 2014年03月 (3)
- 2013年12月 (1)
- 2013年11月 (1)
- 2013年10月 (5)