AD-TECH
- リクルートデータ組織のブログをはじめました。※最新情報はRecruit Data Blogをご覧ください。
- Recruit Data Blogはこちら
アドテクブログ管理者のTanahashiです。本記事では、先日Los Alamos国立研究所(LANL)からArXivに投稿された量子コンピュータD-Waveを用いた非負二値行列因子分解[1]について紹介します。上のデモはこのアルゴリズムをJavaScriptでほぼそのまま実装したものです。アニーリング部分はD-Waveを使う代わりに焼きなまし法で実装しています。LANLは2015年にD-Wave SystemsのD-Wave 2Xを導入しており、アニーリング型量子コンピュータの応用研究を活発に行なっているため、D-Waveユーザとしては是非注目しておきたい研究機関の一つです。
私たちリクルートコミュニケーションズは以前より早稲田大学と量子アニーリングに関する共同研究を進めていましたが、昨年よりD-Wave Systemsと共同研究を開始し、D-Waveを用いた機械学習アルゴリズムの開発やその広告配信への応用に取り組んでいます。また、今年の6月には量子アニーリングに関する世界トップクラスの国際学会Adiabatic Quantum Computing Conference2017が日本で行われ、私たちもD-Waveを用いた機械学習アルゴリズムやレコメンデーション手法について発表する予定です。
行列分解では$n\times m$次元のある行列$V$を二つの行列$W$($n\times r$次元)と$H$($r\times m$次元)の積に分解する操作を考えます。
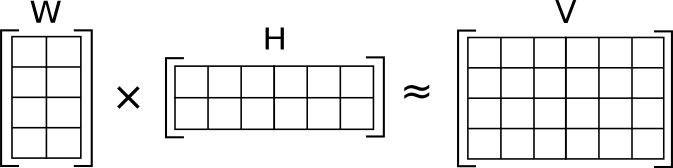
(画像引用: wikipedia)
一般的によく利用される非負値行列分解(NMF)では$W$と$H$の要素が非負であるという条件が加えられます。行列分解をより直観的に理解するために具体例を見てみましょう。
行列分解の具体例
- $n$が画像の次元、$m$が画像のデータ数とすると、$V$の中のi番目の列ベクトル$V_{i}$は$i$番目の画像データを表します。$H$の$i$番目の列ベクトル$h$は$i$番目の画像に対応する低次元表現になります。顔画像の場合、低次元潜在空間を構成する特徴ベクトルを見てみると目や鼻などの顔のパーツが学習されていることがわかります(下図参照)。
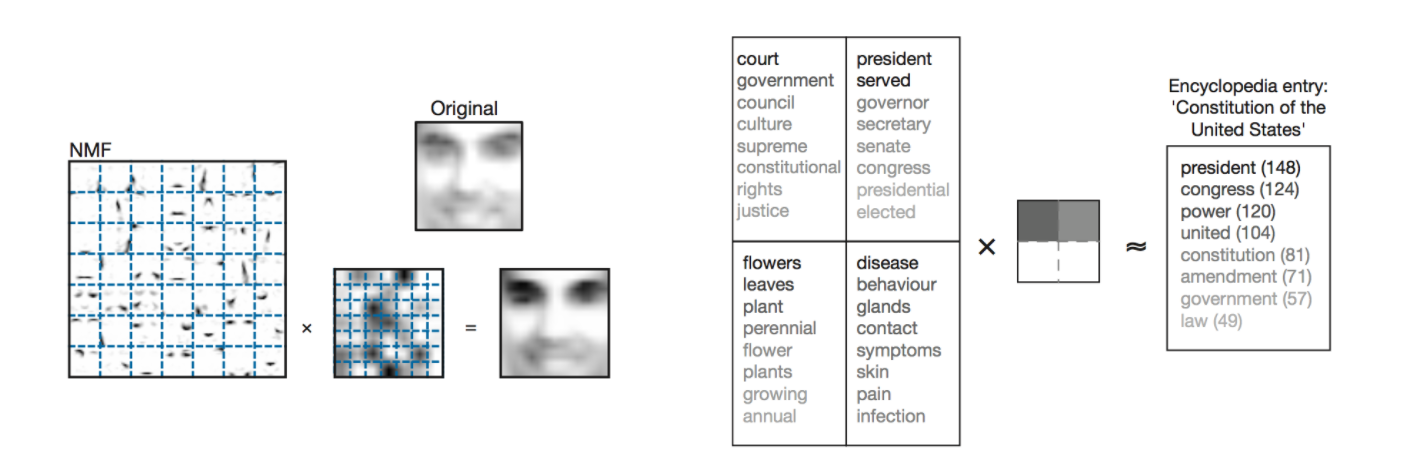
(画像引用: Lee and Seung, 2009)
非負二値行列因子分解(NBMF)
今回LANLが取り組んだ問題は、$W$と$H$が非負であることに加えて、$H$の要素が$0$か$1$しか取らないという条件での行列分解です。
$$ W,H = \mathop{\rm arg~min}\limits_{W, H} \left || V - WH |\right |_{\text{F}} \quad \textrm{s.t.} \quad W_{ij} \ge 0, H_{ij} \in \{0, 1\}$$
NMFと比較したとき、NBMFは以下の特徴を持ちます。
- $H$が離散値をとるため、行列分解は組合せ最適化問題となり解くことが難しくなる。
- $H$が非負の実数値をとる場合(一般的なNMF)と比べて元の行列を復元したときの誤差($ \left || V-WH | \right |_{2}$)は大きくなるが、行列の要素が0と1しかもたないので、少ない情報量でデータを表現することができる
- 0と1はラベルと見ることもできるため、離散的にデータを表現できるという意味でマルチラベル分類とも考えることができる。例えば顧客のセグメント分類などにも利用できる。
1にあるように、既存の手法でこの問題を解くことは難しいのですが、組合せ最適化問題を高速に解くことができるD-Waveを使ってこの問題を解くことを考えます。NMFでよく使われる最適化手法のフレームワークとして交互最小二乗アルゴリズム(ALS)があります。ALSとは、$W$と$H$をお互いに固定しながら交互に最適化する方法です。2つの最適化問題に分割する理由は、分割したそれぞれの副問題の目的関数が最適化しやすい性質を持つようになるためです。NBMFでもALSを利用します。$W$の最適化には射影勾配法[2]などを利用し、$H$の最適化にD-Waveマシンを利用します。
$H$をランダムに初期化
Input : $V,k$
Output : $W,H$
Until 収束
// Wに関する最適化
$W = \mathop{\rm arg~min}\limits_{X \in R+^{n\times r}} \left || V - XH |\right |_{\text{F}} + \alpha \left || X |\right |_{\text{F}}$
// D-Waveを使ってHに関する最適化を行う
$H = \mathop{\rm arg~min}\limits_{X \in \{0, 1\}^{r\times m}} \left || V - WX |\right |_{\text{F}}$
二番目の最適化は、$V$の$i$番目の列ベクトル$V_{i}$と$H$の$i$番目の列ベクトル$H_{i}$に注目すると以下のような副問題に落とし込むことができます。
$$H_{i} = \mathop{\rm arg~min}\limits_{q \in \{0, 1\}^{r}} \left || V_{i} - Wq |\right |_{2}$$
QUBO(二次制約なし二値最適化)への変換
D-Waveによって組み合わせ問題を解くためには、解きたい問題をQUBOと呼ばれる形式に変換してあげる必要があります。 QUBOとは以下の数式で表される最適化問題のことです。
$$x^{*} = \mathop{\rm arg~min}\limits_{x \in \{0, 1\}} \left ( \sum_{i}a_{i}x_{i} + \sum_{i<j}b_{ij}x_{i}x_{j} \right )$$
上で出てきた$H$の最適化は容易にこの形に変換できて、QUBOにおける$a$と$b$は以下のようになります。
$$ a_{j} = \sum_{k}W_{kj} \left ( W_{kj} - 2V_{ij} \right )$$ $$ b_{jk} = 2 \sum_{l}W_{lj}W_{lk}$$
QUBOをD-Waveマシンへどのように配置するか
D-Waveマシンの量子ビットは全ての量子ビットと互いに結合しているわけではないため、残念ながら上で求めたQUBOをそのままD-Waveへ埋め込むことはできません。D-Waveのハードウェア上の量子ビットはキメラ構造をしており、密に繋がった8ビットのユニットが縦横に並んだ構造をしています。キメラ構造によって全結合のQUBOを表現するための手法の一つにEmbeddingがあります。1つの理論ビットを、互いに強結合した複数の物理ビット(鎖)で表現することによってEmbeddingは実現されます。強結合することで同じ鎖に属するビットは常に同じ値を取るように制限されます。下の図では128ビットの4×4キメラ構造を使って16個の理論ビットの全結合を表現した例です。線で繋がった同じ色の量子ビットは鎖を表しています。今回の論文では詳しく述べられていませんが、Embeddingを見つけるためには様々な現実的条件を考慮する必要があります。
実際に考えなければならない問題
- 実際のD-Waveマシンでは歩留まりの問題があり、いくつかのビットは欠損した状態になっているため、下の図のような綺麗な構造を持っているとは限りません。
- Embeddingを探索できたとしても一つ一つの鎖の長さが異なってくると鎖によって物理的な挙動が変わってきます。鎖によって物理的ダイナミクスに偏りが出てしまうと、うまく問題を解くことができなくなってしまう可能性があります。そこで、できるだけ鎖の長さは同じかつ短いことが望まれます。
このような問題を回避するため、欠損ビットが存在する状況で同じ長さの鎖を多項式時間で見つけるアルゴリズム[3]がD-Wave Systemsによって開発されています。
実験結果
NBMFを用いて2,429の顔画像の行列分解を行い、$H$の探索に(1)D-Wave (2)Gurobi (3)qbsolvを利用した場合でアルゴリズムの性能を比較しました。 qbsolvはD-Wave Systemsによって開発されたもので、問題を分割することで高速にタブサーチを行う方法です。
結果をまとめると
- アニーリング回数が1000回以下のときは、D-Waveはqbsolv, Gurobiよりも高速に問題を解くことができた。
- 元の行列の再現性はNMFと比べると劣るが、6.5倍スパースなデータ表現が得られた。
まず、NBMFによってどのような基底$W$が学習されたのかを見てみましょう。

(画像引用: O’Malley, Daniel, et al., 2017)
上の画像の右に並んだ画像群は学習された画像の基底$W$です。通常のNMFでは目や口など部分的なパーツが基底して学習されるケースが見られたのに対して、顔全体を表すものやほぼ黒いものが得られていることがわかります。また、左の画像は元の画像(上)とそのreconstruction(下)を表し、使われた特徴の画像に緑の枠が付いています。NMFでは13%の要素が0のスパースなデータ表現が得られたのに対して、NBMFでは85%が0のスパースなデータ表現が得られました。NBMFでは行列の各要素が1bitで表現されているので、データの容量としては64 * 85 / 13 = 418倍節約できることになります(もとの行列の再現性は低いので一概に比べることはできませんが)。
次に、最適化アルゴリズムごとの計算時間について見てみます。
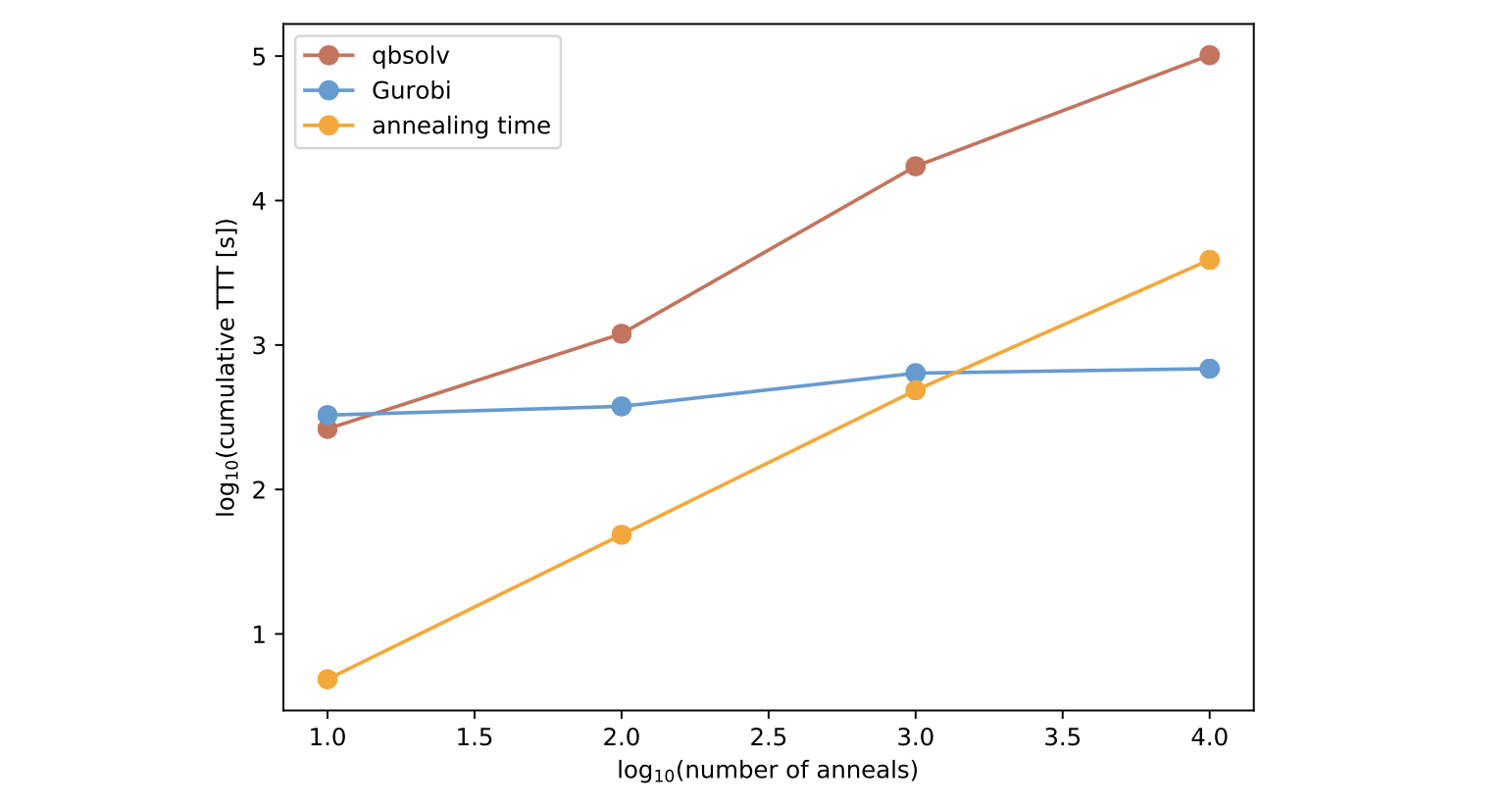
(画像引用: O’Malley, Daniel, et al., 2017)
上のグラフの赤と青のプロットはqbsolvとGurobiの累積TTT(Time-to-target)を表しています。累積TTTとは横軸のアニーリング回数に対応するD-Waveによる最適化と同じ精度の解を見つけるのにどのくらいの時間がかかったのかを表します。オレンジのプロットがD-Waveのアニーリングにかかった時間です。アニーリングの回数が1000回以下の領域ではD-Waveによる最適化が他の2つの手法よりも優れていることがわかります。というのもD-Waveの1回のアニーリングにかかる時間はたった20マイクロ秒であり、1000回最適化を行っても20ミリ秒しかかからないのです。 ただ、少し注意しなければならないのは、ここで示されているアニーリング時間にはチップからのデータの読み込みや問題の書き込み時間は考慮されていないということです。しかし、今後ハードウェアの性能向上に伴い、このような時間は短縮されていくと考えられます。
JavaScriptによるデモ
このページを開いた瞬間になぞの模様が急に動きだしたため、びっくりした方がいたかもしれません。 デモの中では最初に行列$V$がランダムに生成されるのですが、実はその前に$W$と$H$をランダムに生成し、それをかけたものを$V$としています。ですので、本当に最適化がうまく動けば損失を0にすることができるようになっています。しかし見てお分かりの通り、なかなか損失を0にすることはできません。それはなぜか、ぜひ考えてみてください!
まとめ
D-Waveを用いた機械学習のアルゴリズムとして主なものに2009年にGoogleが発表した量子アニーリングによるブースティングアルゴリズム: QBoost[4]があり、さらにLockheed Martinが発表した量子アニーリングによるボルツマンマシン[5]があります。 今回、行列分解が発表されたことで、より多様なアルゴリズムが実現されてきているという印象を受けました。 これからも量子アニーリングによる行列分解の研究が出てくる可能性があると思うのでぜひ注目したいと思います。
Reference
[1] O'Malley, Daniel, et al. "Nonnegative/binary matrix factorization with a D-Wave quantum annealer." arXiv preprint arXiv:1704.01605 (2017).(link)
[2] Lin, Chih-Jen. "Projected gradient methods for nonnegative matrix factorization." Neural computation 19.10 (2007): 2756-2779.(link)
[3] Boothby, Tomas, Andrew D. King, and Aidan Roy. "Fast clique minor generation in Chimera qubit connectivity graphs." Quantum Information Processing 15.1 (2016): 495-508.(link)
[4] Neven, Harmut, et al. "NIPS 2009 demonstration: Binary classification using hardware implementation of quantum annealing." Quantum (2009): 1-17.(link)
[5] Adachi, Steven H., and Maxwell P. Henderson. "Application of quantum annealing to training of deep neural networks." arXiv preprint arXiv:1510.06356 (2015).(link)
TAGS :
#D-WaveARCHIVE
- 月別記事リストを見る
-
- 2020年03月 (2)
- 2019年09月 (3)
- 2019年08月 (1)
- 2019年06月 (1)
- 2019年03月 (5)
- 2019年02月 (3)
- 2018年09月 (1)
- 2018年06月 (2)
- 2018年05月 (2)
- 2018年04月 (1)
- 2018年02月 (1)
- 2018年01月 (1)
- 2017年12月 (2)
- 2017年11月 (1)
- 2017年10月 (1)
- 2017年08月 (1)
- 2017年07月 (2)
- 2017年06月 (1)
- 2017年05月 (3)
- 2017年04月 (5)
- 2017年03月 (12)
- 2017年02月 (16)
- 2017年01月 (1)
- 2016年12月 (1)
- 2016年08月 (1)
- 2016年06月 (5)
- 2016年05月 (2)
- 2016年04月 (1)
- 2016年03月 (3)
- 2016年02月 (8)
- 2016年01月 (3)
- 2015年12月 (2)
- 2015年03月 (1)
- 2015年02月 (2)
- 2015年01月 (3)
- 2014年12月 (2)
- 2014年11月 (3)
- 2014年10月 (1)
- 2014年09月 (2)
- 2014年07月 (1)
- 2014年04月 (2)
- 2014年03月 (3)
- 2013年12月 (1)
- 2013年11月 (1)
- 2013年10月 (5)